Performance
In 2022, researchers P.A. Arts and L. van den Broek published the Fast Continuous Wavelet Transform (fCWT) algorithm, with dramatically positive ramifications for wavelet transform computation. The fCWT enables CoherIQs by scaling down the amount of compute time required for long signals, focusing on the inverse Fourier transform step in the FFT-based implementation of the wavelet transform.
To give an overly brief technical summary of what is going on in the background, this efficient algorithm caches precomputed look-up tables of the iFFT and can apply strategic downsampling to the time-frequency complex matrix prior to the scale dependent operations, allowing large-scale reductions in overall computational complexity. A comprehensive explanation of the fCWT algorithm can be found in the original publication.
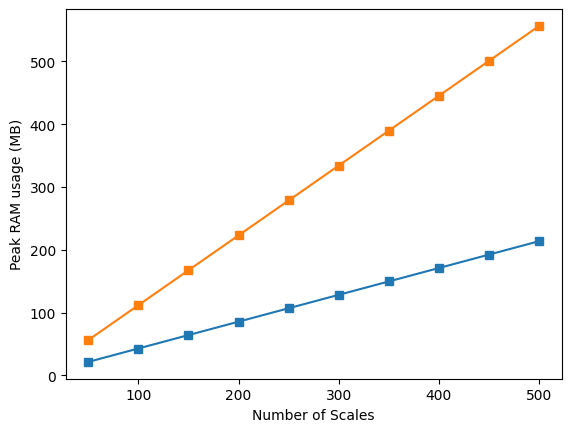
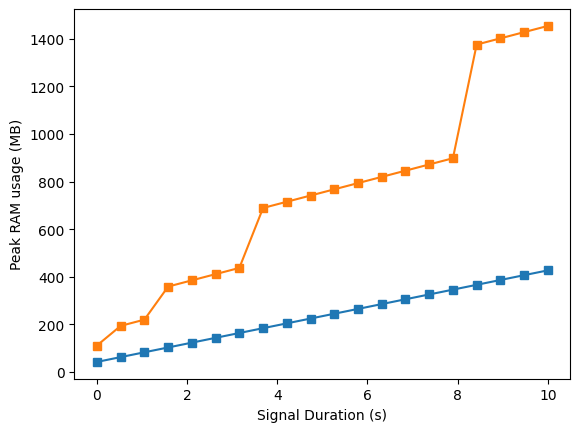
Efficiency comparison in memory usage. Left: increasing frequency resolution. Right: increasing number of samples. Legend: ■ Our model, ■ PyCWT benchmark.
To illustrate the savings realized by these techniques, two signals consisting of pure noise are generated at an 8000 Hz sampling rate. Coherence matrices are then produced using CoherIQs in parallel with the PyCWT library's wavelet coherence transform (WCT) method, which serves as a benchmark for comparison. the efficiency in both domains (time and frequency) is of interest, so we run two experiments. The first figure shows how increasing resolution in the frequency and time domains affects the memory usage. The next figure shows the same two experiments with the memory metric exchanged for compute time, which is where we see the most significant savings.
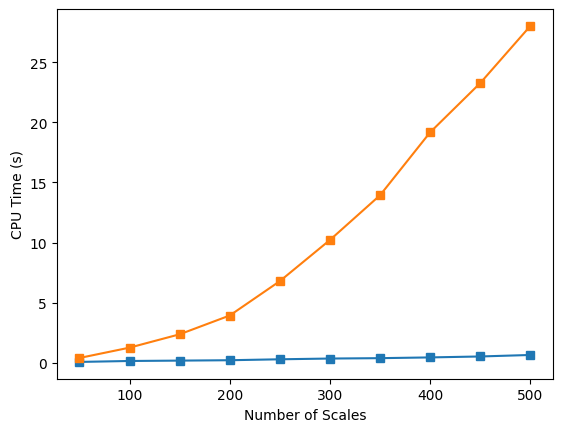
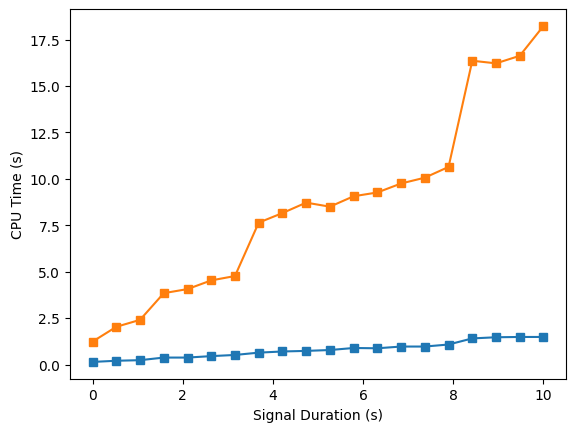
Efficiency comparison in process time. Left: increasing frequency resolution. Right: increasing number of samples. Legend: ■ Our model, ■ PyCWT benchmark.
These results closely replicate the performance findings in the original fCWT publication, showing the large portion of coherence computation being consumed by the supporting wavelet transforms. Additionally, the step-wise behavior observed when increasing signal duration is a well documented phenomena in FFT based implementations, which are most efficient at transforming signals whose input lengths are 2n, n ∈ ℕ. As a result, such algorithms will pad signals to the next power of 2.